多项式的算术性质

我们先来看一下如何将多项式和算术运算关联起来。例如，有两个多项式 \(f(x)\) 和 \(g(x)\)，尝试将他们相乘得到 \(h(x) = f(x) \times g(x)\)，在任意一个 \(x = r\) 处 \(h(x)\) 的计算结果都是 \(f(r)\) 和 \(g(r)\) 的乘积。考虑下面两个多项式 \(f(x) = 2x^2 - 9x + 10\) 和 \(g(x) = -4x^2 + 15 x -9\)。以图形的形式可视化：

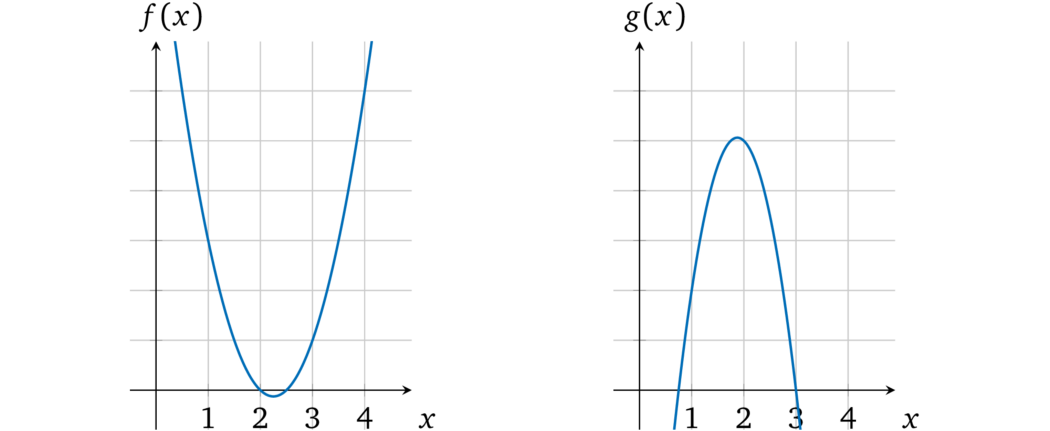
当 \(x = 1\) 时 \(f(1) = 2 -9 + 10 = 3\)，\(g(1) = -4 + 15 -9 = 2\)。

把两个多项式相乘：\(h(x) = f(x) \times g(x) =-8 x^4 + 66 x^3 - 193 x^2 + 231 x -90\)。从图中可以看出相乘的结果：

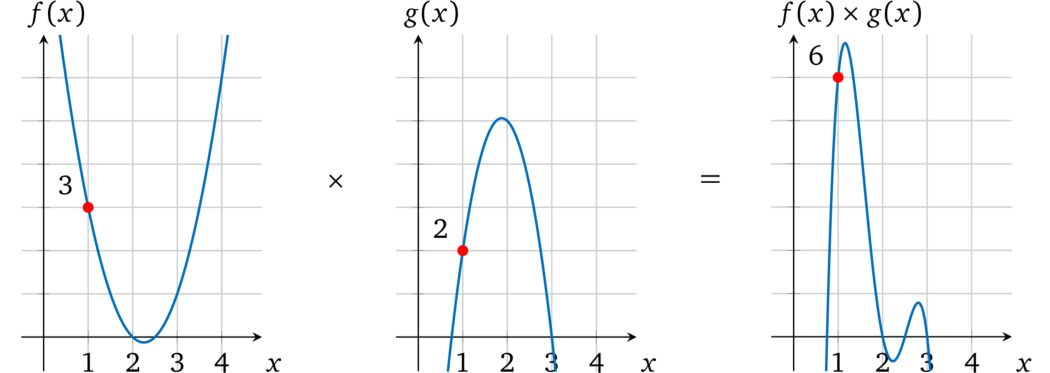
\(x = 1\) 时，计算 \(f(x) \times g(x)\) 结果为：\(h(1) = -8 + 66 -193 + 231 - 90 = 6\)，也就是说当 \(x = 1\) 时，\(h(x)\) 就是 \(f(x)\) 和 \(g(x)\) 相乘的结果 ，在 \(x\) 取其他值的时候也一样。

同样，如果我们将 \(f(x)\) 和 \(g(x)\) 相加，会得到 \(-2x^2 + 6x + 1\)，在 \(x = 1\) 处的计算结果就是 5。

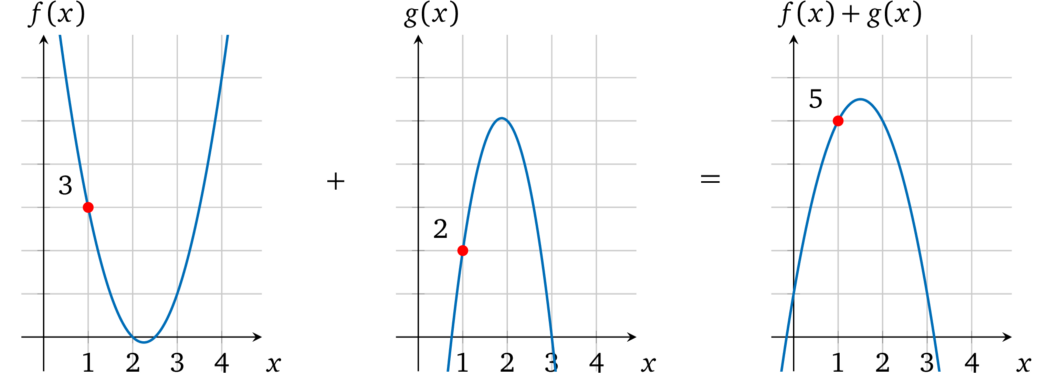
注：在其他 \(x\) 的取值处，多项式相加的计算结果也是将两个多项式的值加在一起的结果，例如可以验证一下 \(x = 2\)、\(x = 3\) 处的结果。

如果我们可以将操作数的值表示为多项式（我们也确实可以这么做），那么利用算术属性，我们就能够得到操作数的计算结果了。

译者注：回忆一下，在「证明的媒介」一节中，我们曾提到过：任何多项式在任意点的计算结果都可以看做是其唯一身份的标识。

反过来，当我们知道某个多项式的时候，也就意味着我们知道多项式上某个点的取值了。这就是借助多项式来完成证明的依据。