变量多项式

使用这种方法，我们可以一次证明许多运算（例如数百万甚至更多），但它有一个严重的缺点。

如果证明过程中执行的「程序」在不同运算中使用了相同的变量作为操作数或作为输出，例如：

$$\color{ForestGreen}{a}\quad \times \quad\color{blue}{b}\quad = \quad\color{red}{r_1}$$

$$\color{ForestGreen}{a}\quad \times \quad\color{blue}{c}\quad = \quad\color{red}{r_2}$$

对于这两个运算，\(\color{ForestGreen}{a}\) 必须在左操作数多项式中表示：

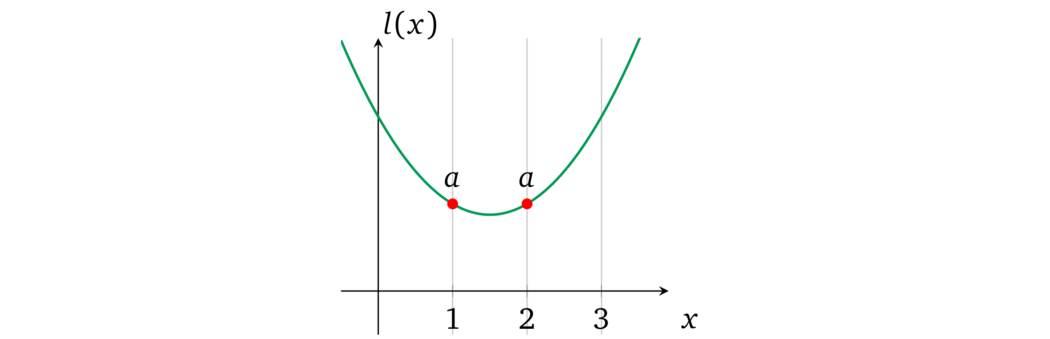
尽管如此，由于我们的协议允许证明者为多项式设置任何系数，所以他为不同的运算（由一些 \(x\) 表示）设置不同的 \(a\) 值是不受限制的，例如：

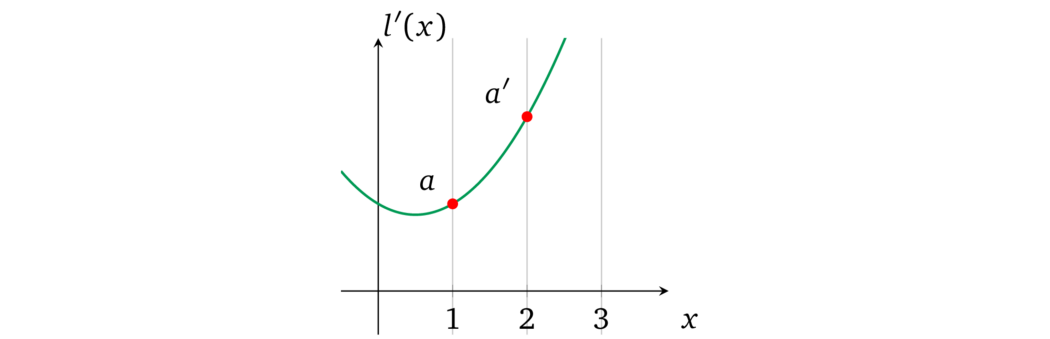
这种自由破坏了一致性，并允许证明者证明验证者不感兴趣的其他程序的执行。因此，我们必须确保任何变量在它被使用的每个运算中只能有一个值。

注：这里的变量与常规的计算机科学中的变量定义不同，这里的变量是不可改变的，而且每次执行都只能被赋值一次。

译者注：请务必注意「变量」的定义，它是程序中的变量，但又不可改变，其实是指示例伪代码中那些不会被修改的变量。在 zk-SNARK 论文中，这个「变量」其实有一个对应的名词叫做 Assignment，是算术电路的「赋值」。而所有的 Assignment 是一个算术电路可满足性问题的解，包含了算术电路的输入值以及电路运算过程中输出的中间结果值。