多个运算
现在我们已经能证明单个运算了,但要怎样扩展才能证明多个运算(这是我们的最终目标)呢?让我们尝试添加另一个运算。假如需要计算乘积:\(a \times b \times c\)。在基本运算模型中,这意味着两个运算:
$$\color{ForestGreen}{a}\quad \times \quad\color{blue}{b}\quad = \quad\color{red}{r_1}$$
$$\color{ForestGreen}{r_1}\quad \times \quad\color{blue}{c}\quad = \quad\color{red}{r_2}$$
在前面的讨论中,我们可以通过使操作数多项式计算为某个任意 \(x\) 处(例如 \(1\))的相应值来表示此类运算。有了这个方法,多项式的属性并不会限制我们在不同的 \(x\) 处(例如 \(2\))表示其他值,即:
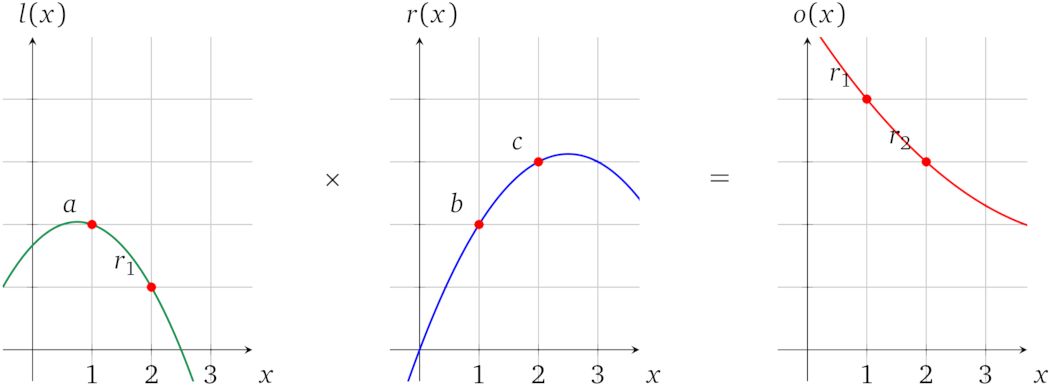
这种独立性允许我们一次执行两个运算而不会将它们「混合」在一起,也就是说相互之间没有干扰。这个多项式算术的结果就变成了:
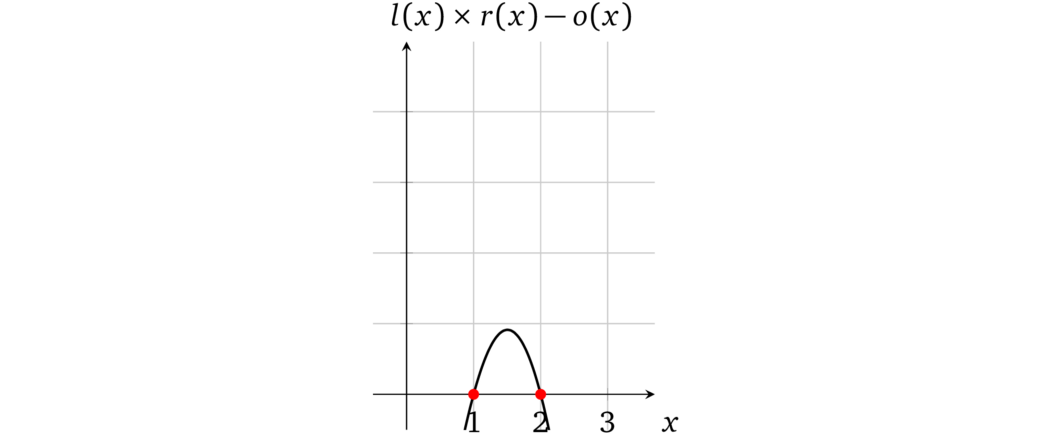
可以看出,运算多项式有两个根 \(x = 1\) 和 \(x = 2\)。因此,这两次计算都被正确执行了。
译者注:这里的示例为了方便理解,选择了 \(x = 1\) 和 \(x = 2\) 两个位置。在完整的 zk-SNARK 方案中,这些「root」值必须为有限域内的随机数,否则就会引入安全漏洞。
我们再来看一个有三个乘法运算的例子 \(2 \times 1 \times 3 \times 2\),它按照下面的步骤执行:
$$\color{ForestGreen}{2}\quad \times \quad\color{blue}{1}\quad = \quad\color{red}{2}$$
$$\color{ForestGreen}{2}\quad \times \quad\color{blue}{3}\quad = \quad\color{red}{6}$$
$$\color{ForestGreen}{6}\quad \times \quad\color{blue}{2}\quad = \quad\color{red}{12}$$
我们需要将它们表示为操作数多项式,对于由 \(x \in \{1, 2, 3\}\) 所表示的计算,\(l(x)\) 相应地经过 \(\color{ForestGreen}{2, 2}\) 和 \(\color{ForestGreen}{6}\)(即经过点 \((1, \color{ForestGreen}{2}), (2, \color{ForestGreen}{2}), (3, \color{ForestGreen}{6})\)),同样 \(r(x) \ni (1, \color{blue}{1}), (2, \color{blue}{3}), (3, \color{blue}{2})\),以及 \(o(x) \ni (1,\color{red}{2}), (2, \color{red}{6}), (3, \color{red}{12})\)。
但是,我们如何找到经过这些点的多项式呢?对于任何超过一个点的情况,都必须使用特定的数学方法。