多项式插值

为了构造操作数和输出多项式，我们需要一种方法，对于给定的一组点可以产生通过所有这些点的弯曲多项式，这种方法被称为插值。有几种不同的方法可以得到这个多项式：

  • 具有未知数的方程组
  • 牛顿多项式
  • 内维尔算法
  • 拉格朗日多项式
  • 快速傅里叶变换

我们以第一个方法为例。这个方法的思路是存在一个系数未知、阶数至多为 \(n\) 的唯一多项式能够经过给定的 \(n + 1\) 个点，对于每个点 \(\left\{ \left(x_i, y_i\right) \right\}_{i \in [n + 1]}\)，多项式在 \(x_i\) 处的计算结果都等于 \(y_i\)。在我们的例子中，三个点对应阶数为 2 的多项式，表示为：

$$ax^2 + bx + c = y$$

让我们令左操作数多项式（绿色）在每个点的多项式求值相等，并通过用其他系数表达每个系数来求解方程组：

img

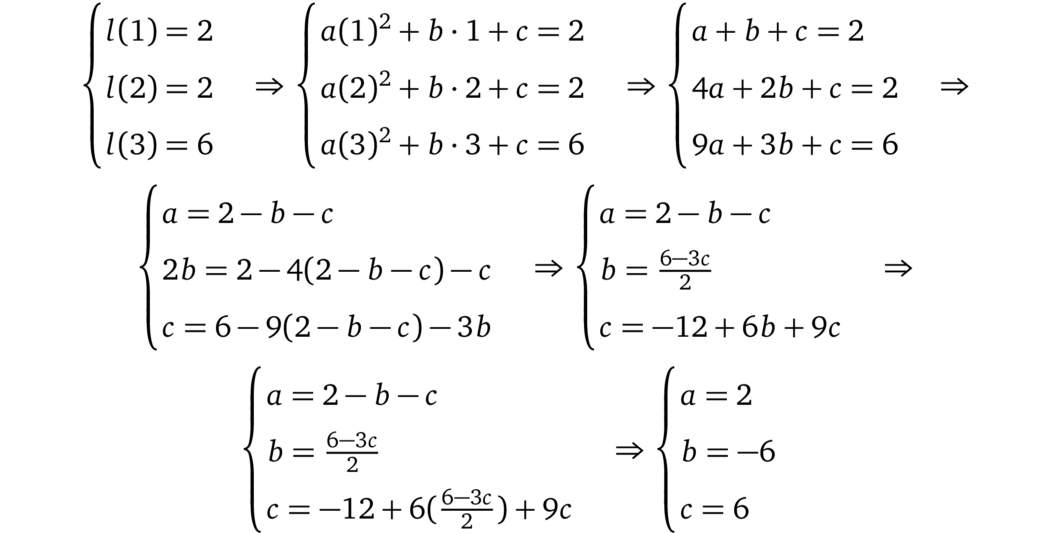
因此左操作数多项式为：

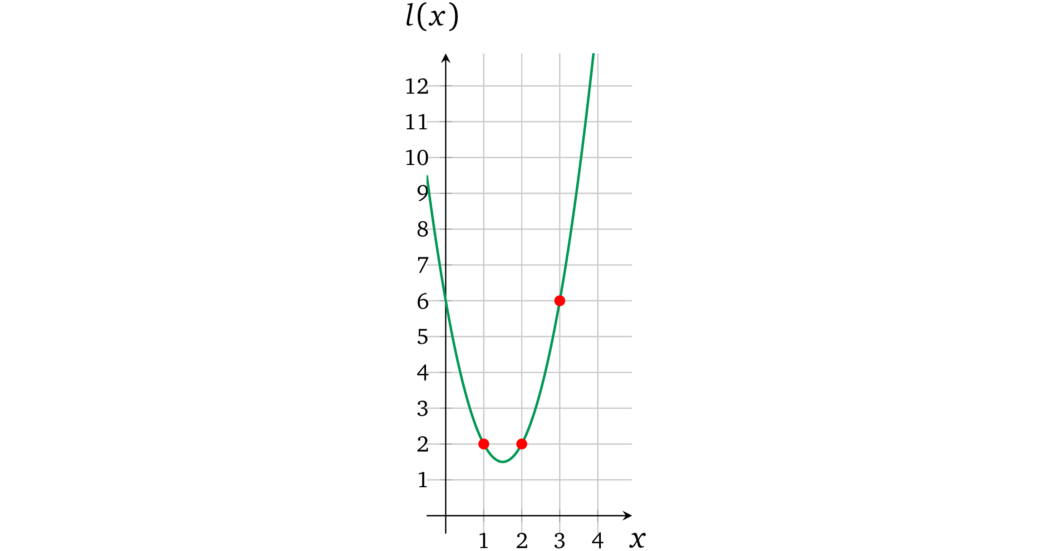
$$\color{ForestGreen}{l(x)} = 2x^2 - 6x + 6$$

对应于下图：

img

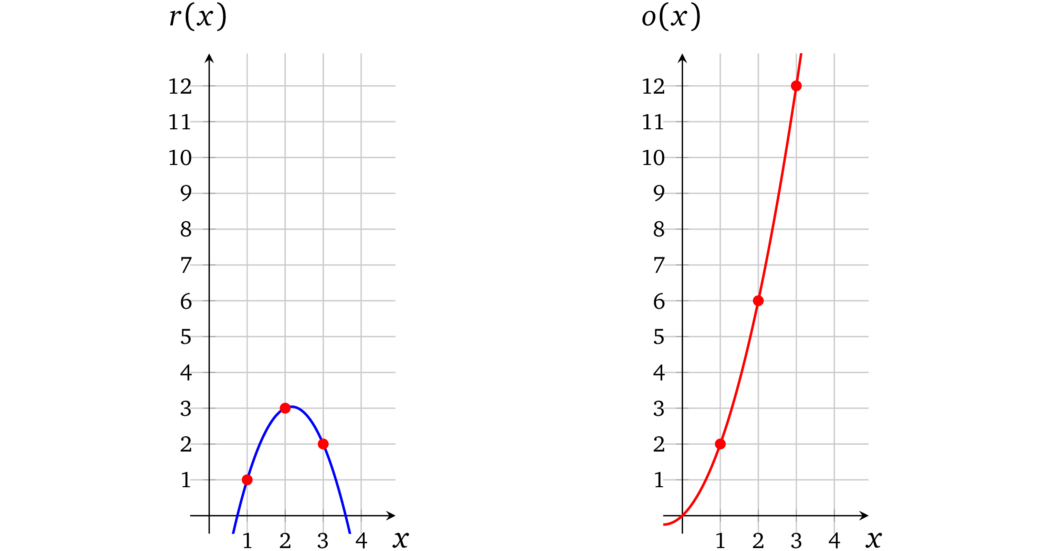
我们可以用同样的方法找到 \(r(x)\) 和 \(o(x)\)：

$$\color{blue}{r(x)} = \frac{-3x^2 + 13x - 8}{2}; \quad \color{red}{o(x)} = x^2 + x$$

img