多运算多项式
现在我们有了代表三个运算的操作数多项式,让我们一步一步地看看如何验证每个运算的正确性。回想一下,验证者正在寻找等式 \(l(x) \times r(x) - o(x) = t(x)h(x)\)。在这种情况下,由于运算在点 \(x \in \{1,2,3\}\) 处表示,因此目标多项式必须在这些 \(x\) 处计算为 \(0\),换句话说,\(t(x)\) 的根必须是 1、2 和 3,其基本形式为:
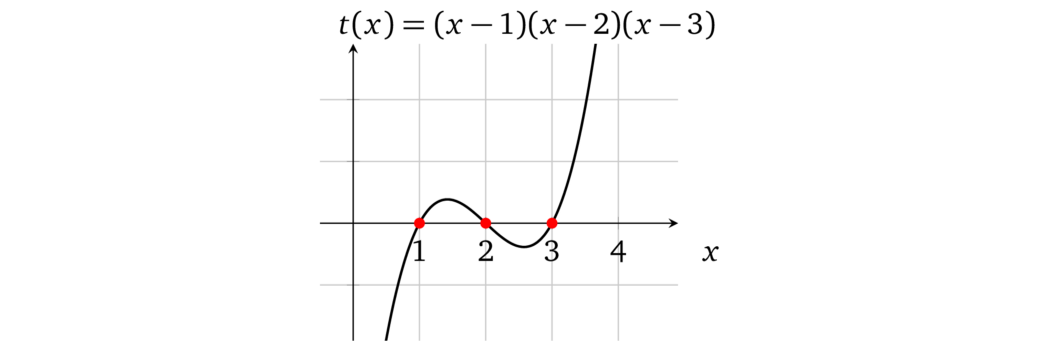
首先,将 \(l(x)\) 和 \(r(x)\) 相乘,得到:
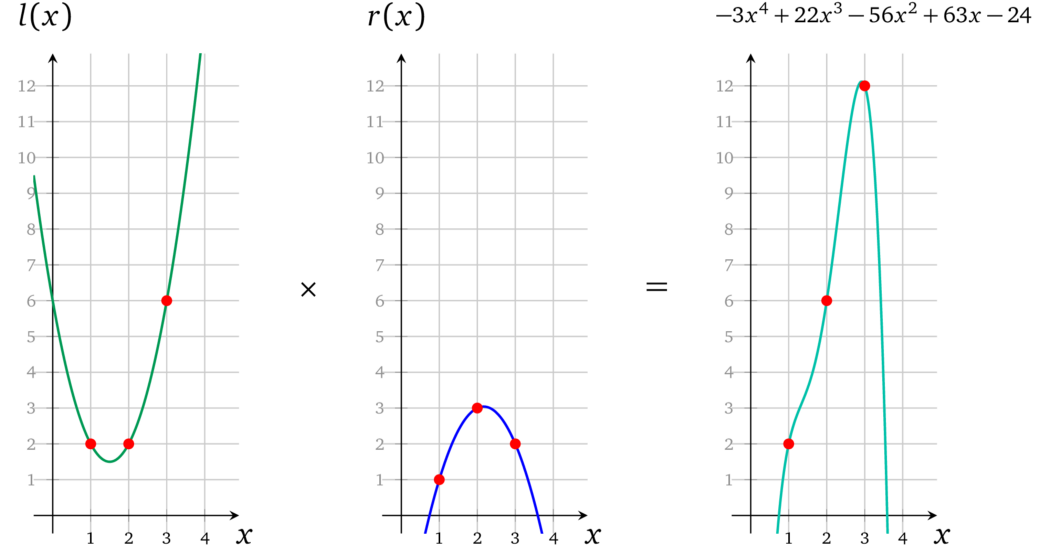
接着,从 \(l(x) \times r(x)\) 的结果中减去 \(o(x)\):
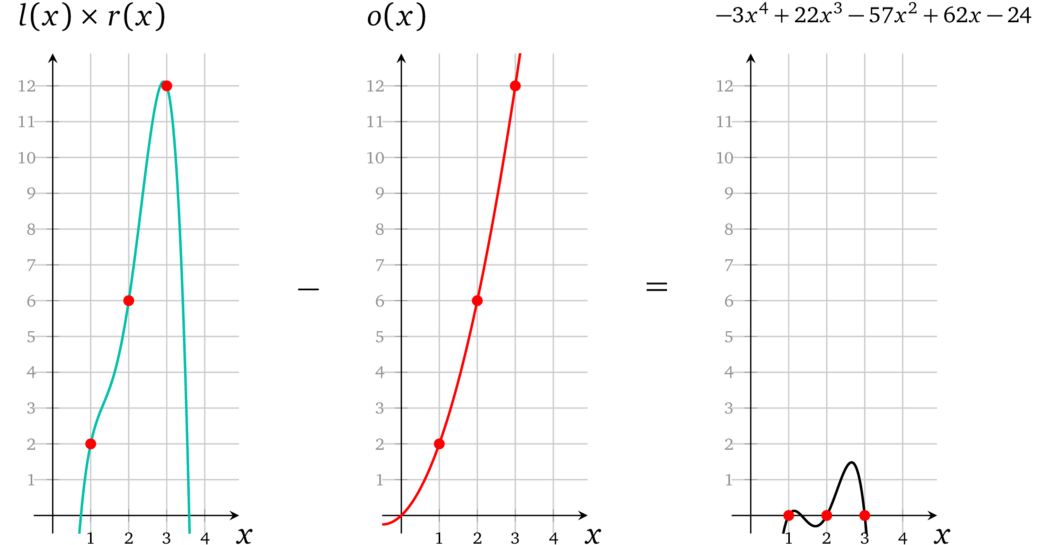
已经可以看出,每个操作数的乘法都对应一个正确的结果。对于最后一步,证明者需要提供一个有效的辅因子:
$$h(x) = \frac{l(x) \times r(x) - o(x)}{t(x)} = \frac{-3x^4 + 22x^3 - 57x^2 + 62x - 24}{(x - 1)(x - 2)(x - 3)}$$
使用长除法我们得到:
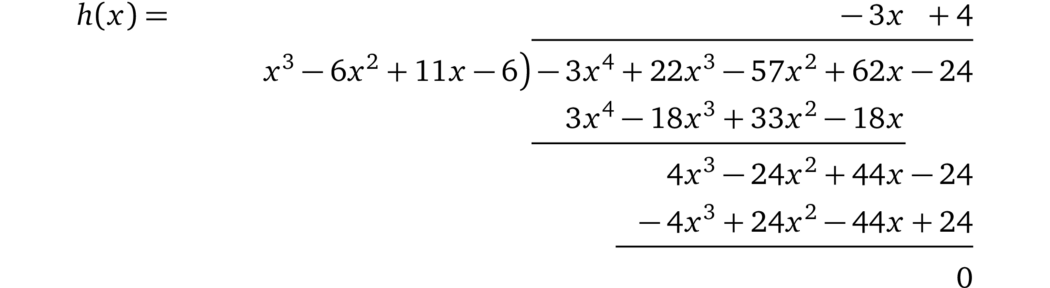
使用 \(h(x) = -3x + 4\),验证者可以计算 \(t(x)h(x)\):
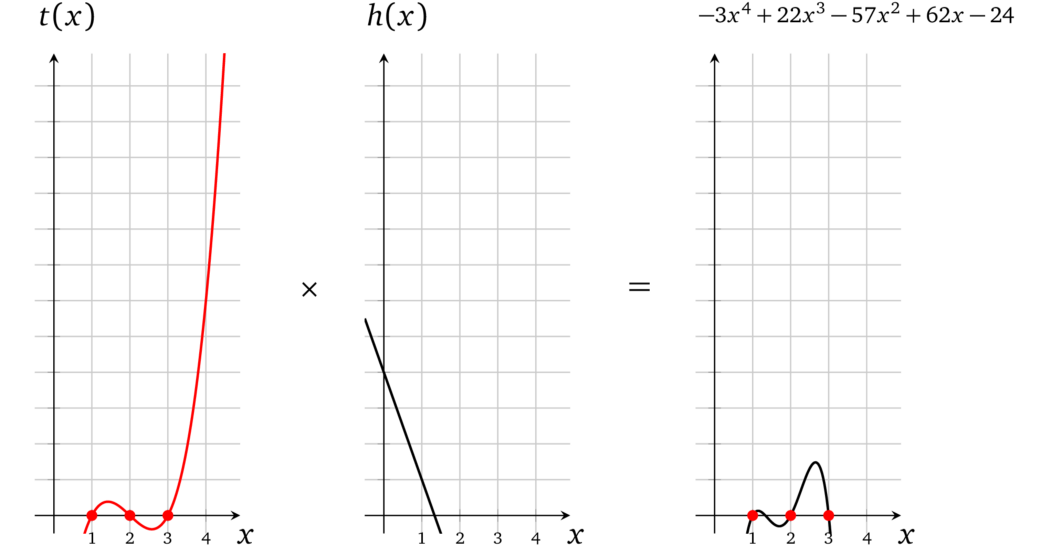
现在很明显 \(l(x) \times r(x) - o(x) = t(x) h(x)\),这就是我们要证明的内容。
译者注:这里只需要一组多项式 \(l(x)\)、\(r(x)\)、\(o(x)\) 就可以表示出所有计算的约束关系,计算的数量与目标多项式 \(t(x)\) 的根的数量相同。
当前的协议似乎存在一些缺陷,只能证明证明者拥有一组多项式 \(l(x)\)、\(r(x)\)、\(o(x)\) 在 \(t(x)\) 几个根的取值处 \(l(x) \times r(x) = o(x)\),无法证明这组多项式符合我们要证明的数学表达式:
多个计算关系是分开表示的,这些算式之间的关系也无法进行约束
由于证明者生成的证明中只有计算结果,左操作数、右操作数、输出在计算中混用也不会被发现
由于左操作数、右操作数、输出是分开表示的,相互之间的关系无法进行约束